«یانیر باریام» معتقد بود که مثال پاروزنان ریچارد داکینز نقص دارد و یک موضوع مهم را در نظر نمی‌گیرد: موقعیت جغرافیایی. گفت فرض کنید وقتی که قایق‌ران‌ها مسابقه را به پایان می‌رسانند و به جمع مسابقه‌دهنده‌ها برمی‌گردند، به جای این که با بقیه مخلوط شوند، به انتهای یک صف وارد شوند. وقتی هم که قایق‌ران‌ها می‌خواهند مسابقه‌ی جدیدی شروع کنند، افراد تیم‌ها را دو نفر دو نفر از سر صف جدا کنیم و سوار قایق کنیم. در این وضعیت چه اتفاقی می‌افتد؟ آیا استفاده از صف به جای یک گروه درهم، تغییری در نتیجه ایجاد می‌کند؟

اگر کسی در صف همسایه‌های هم‌زبان خودش داشته باشد، شانس پیروزی‌اش بیش‌تر است و اگر همسایه‌ها متفاوت باشند، شانس شکست خوردن‌اش بیش‌تر می‌شود. دو همسایه‌ی غیرهم‌زبان کارایی کم‌تری دارند و در نتیجه به احتمال زیاد از جمع حذف می‌شوند.

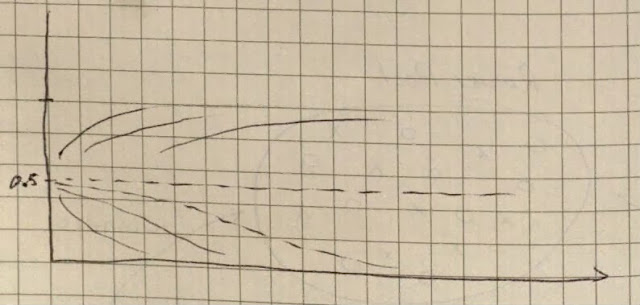
با این ترتیب، بعد از مدتی در صف الگو (pattern) شکل می‌گیرد؛ گروه‌های همسایگی از پاروزنان هم‌زبانی تشکیل شده‌اند که نزدیک به هم هستند (که در اصطلاح به آن‌ها مجموعه‌ای از patch ها می‌گویند). درباره‌ی نمونه‌ای از شکل‌گیری الگو در دو پست قبل نوشتم. شکل زیر به نوعی نشان‌دهنده‌ی یک صف است که در آن الگوها شکل گرفته‌اند.

شکل زیر به نوعی نشان می‌دهد که با در نظر گرفتن موقعیت جغرافیایی، چه طور فضا تقسیم می‌شود و گروه‌هایی با اعضایی که رفتار (یا خصوصیت) مشابه دارند کنار هم شکل می‌گیرند. برای مثال در شکل زیر گروه‌های همسایگی از افراد مشابه تشکیل شده‌اند و در نتیجه در قلم‌روی خودشان توانایی زیستی (fitness) بالاتری دارند.

با این ترتیب وقتی جغرافیا را در نظر می‌گیریم، احتمال بیش‌تری برای شکل‌گیری گوناگونی (diversity) هست. اگر همه با هم مخلوط می‌شدند، بسیاری از بین می‌رفتند و تنها یک گروه باقی می‌ماندند؛ اما حالا که هر یک از گونه‌ها فرصت دارد برای خودش قلم‌رو داشته باشد و با افراد مناسب خودش تعامل داشته باشد، در آن محدوده شانس بیش‌تری برای بقا دارد.

از قرار معلوم یانیر باریام با ریچارد داکینز تلفنی در این مورد صحبت کرده، هرچند که سندی مبنی بر قانع شدن داکینز در دست‌رس نیست.

 یک مسابقه‌ی پاروزنی برپاست. در هر قایق دو نفر پارو می‌زنند و هر نوبت دو قایق با هم مسابقه می‌دهند. در شروع هر مسابقه، چهار نفر را به تصادف از جمع پاروزنان انتخاب می‌کنیم و در دو قایق می‌نشانیم. بازندگان از مسابقه خارج می‌شوند و برندگان دوباره به جمع برمی‌گردند، مثل شکل زیر.

شرکت‌کننده‌ها یا انگلیسی‌زبان هستند و یا آلمانی زبان (در شکل بالا با ضرب‌در و دایره نشان داده شده‌اند). اگر دو پاروزن هم‌زبان باشند، به‌تر با هم هماهنگ می‌شوند و کارایی به‌تری دارند. در نتیجه در شکل بالا به احتمال زیاد قایق بالایی برنده خواهد شد، چون پاروزن‌هایش هم‌زبان هستند.

هرچه‌قدر تعداد انگلیسی‌زبان‌ها بیش‌تر باشد، شانس برنده شدن‌شان هم بیش‌تر است؛ هر بار که به تصادف دو نفر را انتخاب می‌کنیم، احتمال بیش‌تری هست که هر دو نفر انگلیسی‌زبان باشند و به همین ترتیب موفقیت کل انگلیسی‌زبان‌ها ادامه پیدا می‌کند. همین مساله در مورد آلمانی‌زبان‌ها هم درست است.

در این سیستم سه نقطه‌ی تعادل داریم.

یکی از تعادل‌ها این است که تعداد انگلیسی‌زبان‌ها و آلمانی‌زبان‌ها دقیقن برابر باشد و به همین ترتیب برابر هم بماند. این تعادل ناپایدار است (در سیستم‌های دینامیکی به آن unstable fixed point گفته می‌شود). وقتی دو نفر را به تصادف انتخاب می‌کنید، به احتمال بیست و پنج درصد هر دو آلمانی‌زبان هستند، به احتمال بیست و پنج درصد هردو انگلیسی‌زبان و به احتمال پنجاه درصد هم یکی آلمانی‌زبان است و دیگری انگلیسی‌زبان. اما کافی است که تعادل کمی جابه‌جا شود و تعداد یک گروه کمی بیش‌تر از گروه دیگر شود. در نتیجه در انتخاب‌های بعدی گروه با تعداد بیش‌تر شانس بیش‌تری برای برنده شدن دارند و به همین ترتیب تعدادشان بیش‌تر و بیش‌تر می‌شود (و همان‌طور که دیدید تعادل از اول هم پایدار نبود).

دو نقطه‌ی تعادل دیگر هم داریم: به تدریج همه‌ی جمعیت هم‌زبان شوند، چه همه‌ی آلمانی‌زبان‌ها باقی بمانند، چه همه‌ی انگلیسی‌زبان‌ها. فرض کنید همه انگلیسی‌زبان هستند. در این شرایط اگر یک آلمانی‌زبان به جمع اضافه شود، شانسی برای بقا ندارد چرا که حتمن موقع مسابقه با یک انگلیسی‌زبان در قایق خواهد بود و در رقابت با یک قایق که هر دو انگلیسی‌زبان هستند، شکست خواهند خورد. در شکل زیر به طور کیفی می‌بینید که این سه نقطه‌ی تعادل کجا هستند. وسط که ناپایدار است و بالا و پایین (معادل صفر و یک) پایدار هستند. برای مثال در شکل پایین عدد می‌تواند نشان دهد که چه کسری از پاروزن‌ها آلمانی هستند (یا انگلیسی)، محور افقی زمان است و هر خط نشان‌دهنده‌ی تغییرات ترکیب جمعیت در زمان است.

در این مثال فرض کنید «انگلیسی‌زبان بودن» یک ژن است و «آلمانی‌زبان بودن» هم یک ژن. قایق هم به نوعی نماد ارگانیسمی است که دربرگیرنده‌ی ژن‌هاست. وقتی یک قایق در مسابقه پیروز می‌شود، به نوعی ارگانیسم موفق بوده، بقا پیدا کرده و ژن‌هایش فرصت گسترش بیش‌تر پیدا کرده‌اند. بنا بر این مثال، ژن‌ها به تنهایی نه بد هستند و نه خوب. به نوعی این محیط است که تعیین می‌کند چه ژن‌هایی شانس بیش‌تری برای بقا دارند و چه ژن‌هایی حذف می‌شوند.

این مثال تنها برای باز کردن موضوع بود و دقیق نیست. برای نمونه در مورد افزایش جمعیت جمع پاروزنان صحبتی نشد؛ می‌توانیم فرض کنیم که هر بار برنده‌ها به جمع پاروزنان برمی‌گردند، تعدادشان دو برابر می‌شود. این مثال در کتاب «ژن خودخواه» نوشته‌ی «ریچارد داکینز» نوشته شده بود. در پست بعدی درباره‌ی اشکالی می‌نویسم که بر همین مثال وارد شده.

فرض کنید یک گروه بچه در یک مهدکودک دورتادور یک میز گرد نشسته‌اند. بچه‌ها اجازه دارند از دو اسباب‌بازی موجود، ماشین و عروسک، تنها یکی را انتخاب کنند و با آن بازی کنند. بچه‌ها ترجیحی برای اسباب‌بازی‌ها ندارند، به جز این که دوست دارند بتوانند با همسایه‌های‌شان بازی کنند. هر بچه تنها دو همسایه، یکی در سمت چپ و یکی در سمت راستش دارد و علاوه بر خودش، تنها به آن دو نفر توجه می‌کند. اگر همسایه‌ها عروسک دارند، بچه هم عروسک را ترجیح می‌دهد و اگر همسایه‌ها ماشین دارند، ماشین گزینه‌ی به‌تری است.

از بچه‌ها می‌پرسیم که چه اسباب‌بازی‌ای دوست دارند و هرکدام یک چیز انتخاب می‌کند. به همه فرصت می‌دهیم که با توجه به انتخاب همسایه‌ها، ببینند اکثریت گروه سه نفره‌ی هرکدام چه چیزی انتخاب کرده‌اند. فرصت تغییر تصمیم می‌دهیم که اگر خواستند اسباب‌بازی‌ها را عوض کنند. وقتی اسباب‌بازی‌ها را عوض کردند، باز هم فرصت می‌دهیم به همسایه‌ها نگاه کنند و اگر خواستند، تصمیم‌شان را عوض کنند؛ به همین ترتیب ادامه می‌دهیم.

با تکرار این الگوریتم، چه الگویی شکل می‌گیرد؟

طبیعتن به شرایط اولیه (initial conditions) بستگی دارد؛ یعنی بستگی دارد که بار اول بچه‌ها چه اسباب‌بازی‌هایی انتخاب کرده باشند و تغییرات بعد از آن بستگی به انتخاب اول دارد. در شکل‌های زیر فرض کنید دایره‌ی توپر نشان‌دهنده‌ی یک اسباب‌بازی باشد و دایره‌ی توخالی نشان‌دهنده‌ی اسباب‌بازی دیگر. در ضمن به جای نشان دادن انتخاب‌ها (بچه‌ها) در یک دایره (به جای میزی که گرد است)، از یک خط استفاده کرده‌ام؛ فرض کنید دو انتهای خط با هم همسایه هستند. هر سطر هم یک مرحله تصمیم‌گیری را نشان می‌دهد.

ممکن است بعد از تصمیم اول هیچ تغییری صورت نگیرد و همه ترجیح بدهند سر تصمیم اول بایستند. مثل چهار بچه‌ی شکل زیر:

●○○●
●○○●
●○○●
●○○●

هر چه قدر هم که تکرار کنیم و به بچه‌ها فرصت عوض کردن اسباب‌بازی بدهیم، این الگو تغییر نمی‌کند. گاهی ممکن است بعد از چند مرحله، همه با هم به یک نتیجه برسند و یکی از دو اسباب‌بازی را اسباب‌بازی انتخاب کنند. مثل بچه‌های شکل زیر:

●●○●○●○●
●●●○●○●●
●●●●●●●●
●●●●●●●●
●●●●●●●●

 به وضعیت بالا در سیستم‌های دینامیکی نقطه ثابت (fixed point) می‌گویند. ممکن است بچه‌ها در هر مرحله تصمیم‌شان را عوض کنند و هیچ وقت هم به نتیجه نرسند. به چهار بچه‌ی زیر نگاه کنید:

●○●○
○●○●
●○●○
○●○●

به وضعیت بالا در سیستم‌های دینامیکی نوسان (oscillation یا گاهی cycle، با توجه به نوع دینامیک) می‌گویند. یک حالت دیگر (که جالب هم هست) شکل‌گیری الگو است. برای مثال بعضی گروه‌ها با ماشین بازی کنند و بعضی با عروسک و این گروه‌ها در کنار هم بمانند و ادامه دهند. برای مثال به شکل زیر توجه کنید:

○●●○○●○○●○●○●●○○●○○○
○●●○○○○○○●○●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○

 در وضعیت بالا چهار گروه مختلف همسایگی شکل گرفته. بعضی‌ها نظرشان را عوض کردند و روی انتخاب جدید ماندند. یک نفر هم نزدیک به وسط انتخابش را عوض کرد و در مرحله‌ی بعد باز هم عوض کرد و به انتخاب اول برگشت و ثابت شد. در شکل بالا دو گروه همسایه با عروسک بازی می‌کنند و دو گروه همسایه با ماشین.

قانون این مهدکودک (که هرکس به اکثریت خودش و همسایه‌ها توجه کند و تصمیمش را عوض کند) قانون به نسبت ساده‌ای بود. اگر قانون پیچیده‌تر باشد، شاید الگوهای پیچیده‌تری هم ظاهر شوند. اگر به موضوع علاقه دارید، در مورد اتوماتای سلولی (cellular automaton) مطالعه کنید. در دو پست آینده می‌نویسم که شکل‌گیری الگو چه طور در فرگشت (تکامل) موثر است و باعث تنوع گونه‌ها می‌شود.

مرکز کنترل و پیش‌گیری از بیماری‌ها (United States Centers for Disease Control and Prevention) هزینه‌ی چند صد میلیون دلاری کرد که در مورد گسترش آنفلوانزا اطلاعات به دست بیاره. کارشون هم این بود که از تک‌تک دکترها خواسته بودن که آمار بیماران آنفلوانزا رو براشون بفرستن. همون زمان یک گروه با استفاده از داده‌های توییتر خیلی راحت، بدون دردسر و با هزینه‌ی کم تونستن در مورد گسترش آنفوانزا و وضعیت‌اش در اون لحظه اطلاعات به نسبت دقیق و به مراتب به‌روزتری کسب بکنن.

اما موضوع به این سادگی هم نیست. به محض این که خبر این استفاده‌ی خارق‌العاده از توییتر به روزنامه‌ها رسید، کاربران توییتر در موردش توییت کردن. چنان توییت‌ها در مورد آنفلوانزا زیاد شد که توییتر رو تحت تاثیر قرار داد و دیگه امکانش نبود با استفاده از توییتر در مورد آنفلوانزا اطلاعات قابل اعتمادی کسب کرد!

متن بالا از گفته‌های «کاوان کپس» از اداره‌ی آمار و سرشماری بود. سخن‌ران می‌گفت درسته که ممکنه داده‌های شبکه‌های اجتماعی با هزینه‌ی کم‌تر و تلاش کم‌تر بتونن نتیجه‌های به‌روزتر و دقیق‌تری تولید کنن، اما هم‌چنان مشکل پابرجاست که این داده‌ها خیلی هم قابل اعتماد نیستن و می‌تونن به همون راحتی که اومده‌ان، به همون راحتی هم برن.

در کشورهایی که ماشین‌ها از سمت راست حرکت می‌کنن، پیش‌فرض کمابیش اینه که عابرهای پیاده هم وقتی به هم نزدیک می‌شن، از سمت راست حرکت بکنن (دست کم فرض من اینه). حدس می‌زنم در همه‌ی کشورهایی که از سمت چپ رانندگی می‌کنن هم جهت حرکت عابرهای پیاده از سمت چپ باشه.

هم‌کار ژاپنی‌مون می‌گفت در ژاپن عابرها سعی می‌کنن از سمت چپ حرکت کنن و روی پله‌برقی هم طرف چپ بایستن تا کسانی که می‌خوان سریع‌تر از پله‌ها بالا برن، از سمت راست سبقت بگیرن. اما در غرب اوساکا قضیه برعکسه: دو عابر وقتی به هم برخورد می‌کنن، هرکدوم به سمت راست خودش حرکت می‌کنه. همین‌طور ملت روی پله برقی طرف راست می‌ایستن تا کسانی که می‌خوان سریع‌تر برن، از سمت چپ سبقت بگیرن.

هم‌کار ژاپنی در مورد علت این پدیده چیزی نمی‌دونست. من خیلی فکر کردم و به نتیجه‌ای نرسیدم که چرا باید مردم در غرب اوساکا بر خلاف بقیه‌ی کشور عمل بکنن (البته شاید جاهای دیگه‌ای هم شبیه به این در ژاپن باشن؛ من خبر ندارم). تنها حدسی که می‌زنم اینه: در پست قبل نوشتم که حرکت عابران مثل یک بازی می‌مونه که دو نقطه‌ی تعادل داره. مهم نیست که کدوم تعادل انتخاب بشه، تا وقتی که هر دو نفر یک تصمیم مشترک بگیرن، سودشون بیشینه می‌شه و نیازی به تغییر استراتژی نمی‌بینن. حالا فرض کنین یک عابر جدید به یک شهر اضافه بشه. عابر ترجیح می‌ده جهت حرکتش طوری باشه که کم‌ترین برخورد رو با دیگران داشته باشه. در نتیجه اگر اکثریت از راست حرکت می‌کنن، به نفع عابره که از راست حرکت کنه، در غیر این صورت که از چپ حرکت کنه. تصمیم عابر باعث می‌شه تعداد اکثریت باز هم بیش‌تر بشه و عابر بعدی انگیزه‌ی بیش‌تری داشته باشه که از راست حرکت کنه و به همین ترتیب پیش می‌ره تا کل مردم منطقه به نفع‌شونه از سمت راست حرکت کنن. شاید در غرب اوساکا هم به صورت اتفاقی، چند نفری از سمت راست حرکت کردن و به همین خاطر حرکت از سمت راست غالب شد.

نمونه‌ی بازخورد (فیدبک) مثبت رو در خیلی امور روزمره می‌بینین:

• کسی که کارهای تلنبار شده زیاد داره و همین حجم زیاد کار، فکرش رو مشغول‌تر می‌کنه. به همین خاطر بازده‌اش پایین‌تر میاد و حجم کارهای تلنبار شده از قبل هم بیش‌تر می‌شه و به همین ترتیب
• کسی که بدهی داره و باید بهره‌ی بدهی‌اش رو بپردازه و در نتیجه بیش‌تر از قبل بدهکار می‌شه و به دنبالش بهره‌ی بدهی‌هاش هم بیش‌تر می‌شه
• کسی که رابطه‌ی موفقی با اطرافیانش برقرار می‌کنه و بازخورد مثبت می‌گیره و روابطش رو باز هم به‌بود می‌ده و خودش و اطرافیان از این رابطه‌ی موفق بیش‌تر استفاده می‌کنن و همین موضوع خودش باعث به‌تر شدن بیش‌تر رابطه می‌شه

در سیستم‌های پیچیده بازخورد (فیدبک) منفی هم وجود داره (وگرنه که یک سیستم ساده است). کسی که کارهای تلنبار شده داره، شاید زندگی‌اش تا جایی بدتر و بدتر بشه و از جایی به خودش بیاد و تلاش‌اش رو برای به‌بود وضعیت‌اش به صورت ناگهانی (و غیر خطی) افزایش بده. یا کسی که بدهی داره، شاید تصمیم بگیره راه‌هایی رو امتحان کنه که از این سیر قهقرایی بیرون بیاد. رابطه‌ی موفق هم تا حدی به‌بود پیدا می‌کنه و بالاخره جایی اشباع می‌شه.