یک مسابقه‌ی پاروزنی برپاست. در هر قایق دو نفر پارو می‌زنند و هر نوبت دو قایق با هم مسابقه می‌دهند. در شروع هر مسابقه، چهار نفر را به تصادف از جمع پاروزنان انتخاب می‌کنیم و در دو قایق می‌نشانیم. بازندگان از مسابقه خارج می‌شوند و برندگان دوباره به جمع برمی‌گردند، مثل شکل زیر.

شرکت‌کننده‌ها یا انگلیسی‌زبان هستند و یا آلمانی زبان (در شکل بالا با ضرب‌در و دایره نشان داده شده‌اند). اگر دو پاروزن هم‌زبان باشند، به‌تر با هم هماهنگ می‌شوند و کارایی به‌تری دارند. در نتیجه در شکل بالا به احتمال زیاد قایق بالایی برنده خواهد شد، چون پاروزن‌هایش هم‌زبان هستند.

هرچه‌قدر تعداد انگلیسی‌زبان‌ها بیش‌تر باشد، شانس برنده شدن‌شان هم بیش‌تر است؛ هر بار که به تصادف دو نفر را انتخاب می‌کنیم، احتمال بیش‌تری هست که هر دو نفر انگلیسی‌زبان باشند و به همین ترتیب موفقیت کل انگلیسی‌زبان‌ها ادامه پیدا می‌کند. همین مساله در مورد آلمانی‌زبان‌ها هم درست است.

در این سیستم سه نقطه‌ی تعادل داریم.

یکی از تعادل‌ها این است که تعداد انگلیسی‌زبان‌ها و آلمانی‌زبان‌ها دقیقن برابر باشد و به همین ترتیب برابر هم بماند. این تعادل ناپایدار است (در سیستم‌های دینامیکی به آن unstable fixed point گفته می‌شود). وقتی دو نفر را به تصادف انتخاب می‌کنید، به احتمال بیست و پنج درصد هر دو آلمانی‌زبان هستند، به احتمال بیست و پنج درصد هردو انگلیسی‌زبان و به احتمال پنجاه درصد هم یکی آلمانی‌زبان است و دیگری انگلیسی‌زبان. اما کافی است که تعادل کمی جابه‌جا شود و تعداد یک گروه کمی بیش‌تر از گروه دیگر شود. در نتیجه در انتخاب‌های بعدی گروه با تعداد بیش‌تر شانس بیش‌تری برای برنده شدن دارند و به همین ترتیب تعدادشان بیش‌تر و بیش‌تر می‌شود (و همان‌طور که دیدید تعادل از اول هم پایدار نبود).

دو نقطه‌ی تعادل دیگر هم داریم: به تدریج همه‌ی جمعیت هم‌زبان شوند، چه همه‌ی آلمانی‌زبان‌ها باقی بمانند، چه همه‌ی انگلیسی‌زبان‌ها. فرض کنید همه انگلیسی‌زبان هستند. در این شرایط اگر یک آلمانی‌زبان به جمع اضافه شود، شانسی برای بقا ندارد چرا که حتمن موقع مسابقه با یک انگلیسی‌زبان در قایق خواهد بود و در رقابت با یک قایق که هر دو انگلیسی‌زبان هستند، شکست خواهند خورد. در شکل زیر به طور کیفی می‌بینید که این سه نقطه‌ی تعادل کجا هستند. وسط که ناپایدار است و بالا و پایین (معادل صفر و یک) پایدار هستند. برای مثال در شکل پایین عدد می‌تواند نشان دهد که چه کسری از پاروزن‌ها آلمانی هستند (یا انگلیسی)، محور افقی زمان است و هر خط نشان‌دهنده‌ی تغییرات ترکیب جمعیت در زمان است.

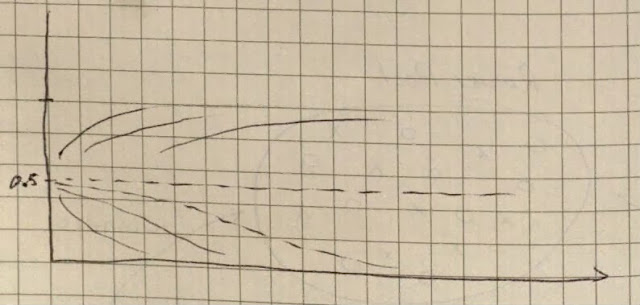در این مثال فرض کنید «انگلیسی‌زبان بودن» یک ژن است و «آلمانی‌زبان بودن» هم یک ژن. قایق هم به نوعی نماد ارگانیسمی است که دربرگیرنده‌ی ژن‌هاست. وقتی یک قایق در مسابقه پیروز می‌شود، به نوعی ارگانیسم موفق بوده، بقا پیدا کرده و ژن‌هایش فرصت گسترش بیش‌تر پیدا کرده‌اند. بنا بر این مثال، ژن‌ها به تنهایی نه بد هستند و نه خوب. به نوعی این محیط است که تعیین می‌کند چه ژن‌هایی شانس بیش‌تری برای بقا دارند و چه ژن‌هایی حذف می‌شوند.

این مثال تنها برای باز کردن موضوع بود و دقیق نیست. برای نمونه در مورد افزایش جمعیت جمع پاروزنان صحبتی نشد؛ می‌توانیم فرض کنیم که هر بار برنده‌ها به جمع پاروزنان برمی‌گردند، تعدادشان دو برابر می‌شود. این مثال در کتاب «ژن خودخواه» نوشته‌ی «ریچارد داکینز» نوشته شده بود. در پست بعدی درباره‌ی اشکالی می‌نویسم که بر همین مثال وارد شده.